体积为零、表面积无穷大的门格尔海绵,居然还能用在现实中!

要充分领会门格海绵的奇妙之处,理解豪斯多夫维数的概念会有所帮助如果你熟悉度量空间和维数的计算!广义上讲,豪斯多夫维数 是粗糙度的度量。它以德国数学家 Felix Hausdorff 的名字命名,通常缩写为 dim_𝐻,用作对象(或集合)如何缩放的度量。虽然推导过程很深奥,计算也很复杂,但为了简单说明其工作原理,我们可以看看科赫曲线。它以瑞典数学家 Neils Fabian Helge von Koch 的名字命名,他在发明这种形状时一直在研究连续、不可微的曲线。
图 1 显示了形状的生成。从直线开始,在第 1 级中我们:
1) 移除中间的三分之一,
2) 用由两段组成的帐篷形状替换它,每段长度为线的 1/3。
为了获得下一级的缩放,我们只需重复上述步骤 1 和 2 来替换当前级别中的每条直线。
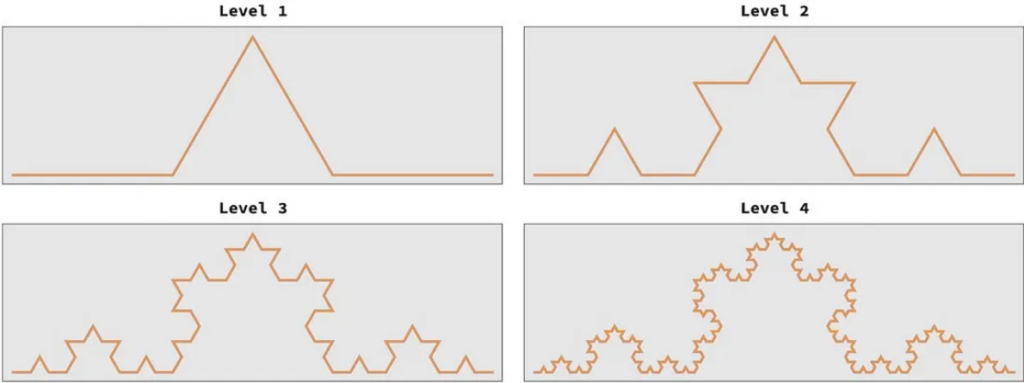
因为它是由 4 个副本构成的,每个副本按 1/3 的比例缩放,所以我们可以使用相似度 d 的关系快速计算出它的豪斯多夫维数,
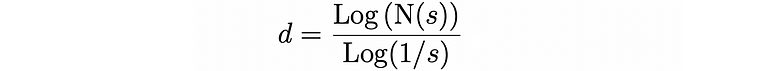
其中 N( s ) 表示副本数,1/ s表示缩放因子。这给了我们:
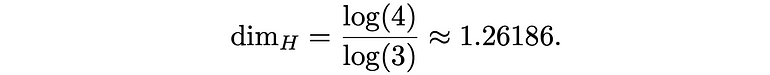
维度告诉我们,形状不仅仅是一条简单的线,也不仅仅是一个平面,还进一步量化了它填充平面的倾向。重要的是,dim_ H告诉我们,尝试将曲线测量为一维线将得到无限的长度,而尝试将其测量为平面物体将得到等于零的面积。因此,豪斯多夫维度是合适的度量。
通往门格尔海绵之路
德裔俄罗斯数学家格奥尔格·康托 (Georg Cantor) 被誉为现代集合论的创始人。1883 年,他发表了一篇论文“Über unendliche, lineare Punktmannigfaltigkeiten V”(“论无限线性点流形,第 5 部分”)。在这篇文章中,他描述了一种构造奇妙的反直觉集合的方法,该集合是无限的、不可数的,但根本不包含任何区间。它通常被称为“康托中间三分之一集”。构造方法如下:
- 从闭区间C ₀ = [0, 1]开始。闭区间包括它们的端点。
- 删除中间三分之一。这与删除开区间 (1/2, 2/3) 相同。剩下的是
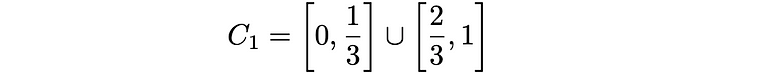
其中“⋃”表示集合的并集。
3. 现在,我们删除剩余区间的中间三分之一,剩下
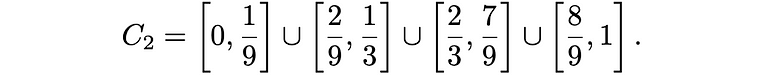
删除剩余区间的中间三分之一以生成C ₙ的过程将无限期地持续下去。当n → ∞时,结果就是通常所称的“康托集”或“康托三元集”。
整个过程如下,从单位线开始,经过四个级别:

康托集具有非凡的性质。首先,康托表明,尽管我们已经删除了无数个区间,但剩下的部分是不可数的,因为它具有与实数集 ℝ 相同的基数。它也是“无处稠密的”,这意味着,由于我们已经删除了所有区间,因此不存在剩余的连续区域。
令人惊讶的是,虽然它是不可数的,但移除的区间的总和为 1,这意味着该集合的“测度”为零。通过对代表移除区间的相应几何级数S求和,很容易看出这一点:
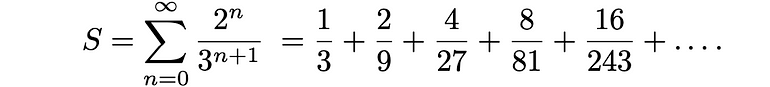
使用标准公式a = 1/3 和r = 2/3,我们发现
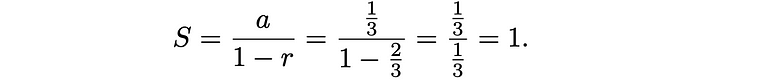
我们总共删除了 1 的长度!
由于它用两个部分代替了三个部分,每个部分的长度都是原始长度的三分之一,因此该构造的豪斯多夫维数等于
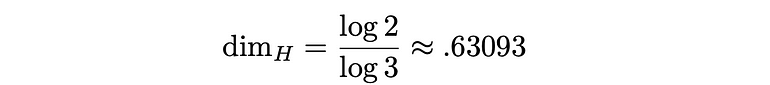
这表明它大于一个点但小于一条线。
但康托集只是这段旅程的第一站。瓦茨瓦夫·谢尔宾斯基是一位波兰数学家,他也对具有反直觉性质的集合感兴趣。他最著名的构造是“谢尔宾斯基三角形”(或“谢尔宾斯基垫片”),它由三个自身的副本组成,每个副本都按 1/2 的倍数缩放:
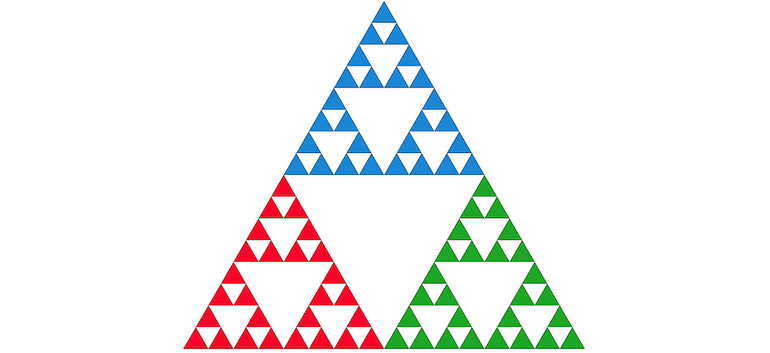
谢尔宾斯基对康托尔的作品十分着迷。1916 年,他写了一篇论文,题为《论康托尔曲线,该曲线包含任意给定曲线的一对一连续像》。在论文中,他将康托尔三元集扩展为二维,形成我们现在所称的“谢尔宾斯基地毯”。地毯的构造过程与康托尔集类似。步骤如下:双语et continue de toute courbe donnée”(“关于包含任何给定曲线的一对一和连续图像的康托曲线”)。在这篇文章中,他将康托三元集扩展为二维,形式就是我们现在所说的“谢尔宾斯基地毯”。地毯的构造过程与康托集类似。步骤如下:
- 从单位正方形开始。
- 将其分成 9 个小方块,每个方块为 3×3。
- 移除中心正方形,留下其他八个小正方形。
- 无限重复此过程。
如果S ₀ 是初始平方,则第n次迭代由Sₙ给出,递归定义为
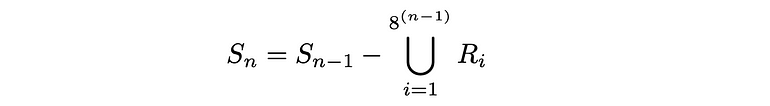
其中Rᵢ表示每次迭代中移除的中心方块。
前四个级别如下所示。为了便于参考,我在底部添加了代表康托分区的条形,其中移除的间隔对应于每个级别移除的方块的宽度:
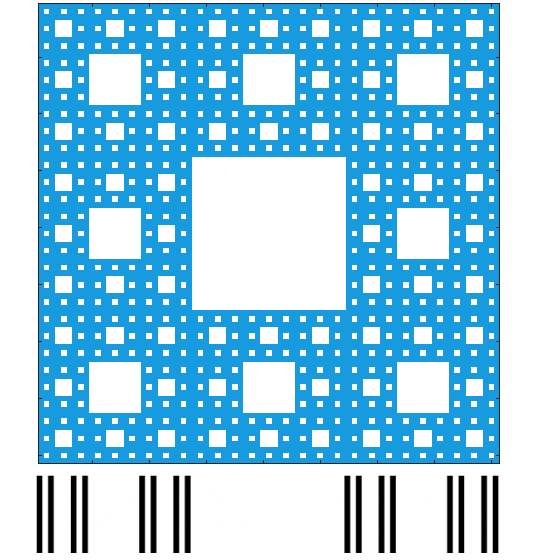
因为它用 8 个部分代替了 9 个部分,每个部分的长度都是原始长度的三分之一,所以该构造的豪斯多夫维数为
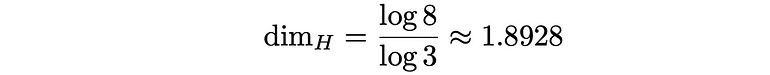
这表明它大于一条线但小于一个平面。
卡尔·门格尔
1926 年,奥地利数学家卡尔·门格尔在探索拓扑集的性质时发表了一篇题为“Allgemeine Räume und Cartesische Räume. I”(“一般空间和笛卡尔空间,I”)的论文。在这篇论文中,他开发了康托三元集的三维类似物。它是最早的三维分形构造之一。
以下是生产门格海绵的步骤:
- 从一个边长为L的立方体开始。
- 将立方体分成 27 个小立方体,每个小立方体的边长为L /3,形成 3 x 3 x 3 的立方格。
- 将中央立方体连同中间的立方体从 6 个面中分别移除。现在剩下 20 个立方体。
- 无限重复此过程。
如果M ₀ 是初始立方体,则第n次迭代M ₙ的一般公式为
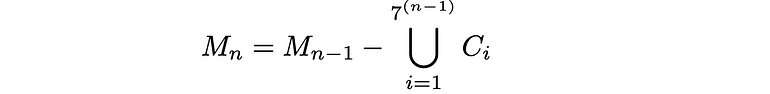
其中C ᵢ是每一步移除的子立方体。
从一个实心立方体开始,以下三次迭代如下所示:
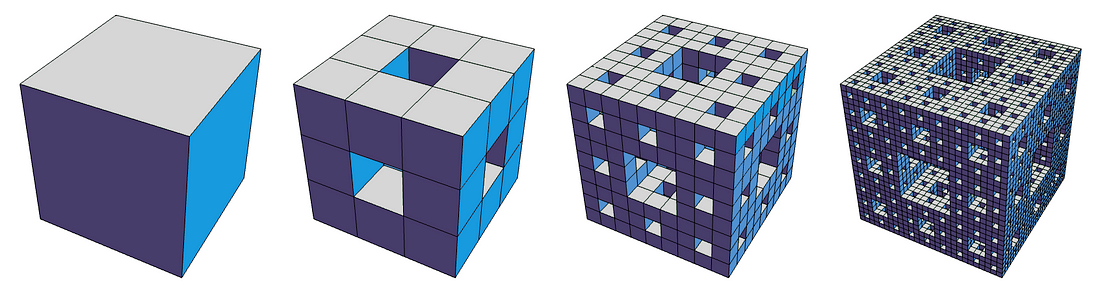
在这种构造中,我们可以看到每个面都是一张谢尔宾斯基地毯,并且通过任意面的中线的路径标记了一个康托集。
虽然表面积随着每次迭代而增加(无约束),但体积却在减小。如果V ₀ 是初始体积,则在步骤n时,体积由下式给出:
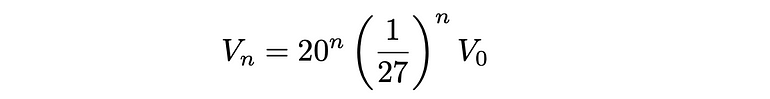
这样当 n → ∞ 时,V ₙ → 0。
马槽海绵的表面积为无限大,体积为零,这一事实由其豪斯多夫维数决定。由于它用 20 个部分代替了 27 个部分,每个部分的长度都是原始边长的三分之一,
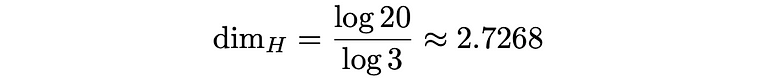
这表明它比平面形状占用的面积更大,但比立体形状占用的体积更小。
鉴于前面这些例子,这并不太令人惊讶。在第一种情况下,我们有一组零维点,它们有点像线。在第二种情况下,我们有一组一维线,它们有点像平面。
对于门格尔海绵,我们可能认为我们看到的是一组二维平面,它们有点像体积。然而,门格尔在 1926 年的论文中证明,他的构造令人惊奇地是拓扑一维的。然而,门格尔在 1926 年的论文中证明,令人惊奇的是,他的构造在拓扑上是一维的。
本质上,这是因为随着表面积的增加,每个表面都会被彻底刺穿。在极限情况下,最终既没有体积也没有表面积——只剩下一条非常“弯曲”的线。这条曲线的拓扑维数为 1。换句话说,门格海绵的勒贝格覆盖维数为 1。
勒贝格覆盖维数给出了定义拓扑维数的严格方法。由于对于孟格海绵,它等于 1,这立即意味着所有一维曲线都包含在其中。因此,它是一条通用曲线。对于所有可以在二维中绘制的曲线,谢尔宾斯基地毯也是如此。但是,由于海绵是在三维中构建的,因此它还可以包含不仅仅是平面的图形,并且可能嵌入到更高维度中。
最近的一项研究结果证明了所有结都可以在门格海绵中找到,这是这种普遍性的一个绝佳例子!