您是否想过如何进行量子力学实验？您是否认为这需要复杂的设备？在这里，您可以了解如何进行光电效应实验以及如何使用现成的材料测量普朗克常数。

LED 的工作原理

发光二极管 ( LED ) 的工作原理与二极管类似。它的作用类似于水的液压阀：二极管只允许电流朝一个方向流动。考虑以下电路：

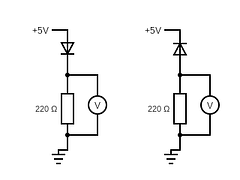
左侧电路中有电流流动，从理论上讲，二极管表现为完美导体，而右侧电路中没有电流流动，二极管表现为开路（或者，如果您愿意，也可以说是一个无限大电阻）。左侧电路的电压表显示电压接近 5V（略低一些，因为 LED 在允许电流流动时产生的电阻很小）。右侧电路的电压表读数几乎为零（不是完全为零，因为 LED 表现为具有巨大电阻的电阻器）。LED 的工作原理也一样。与普通二极管的唯一区别在于，当电流流动时，它会发光。

光电效应

如果我们像右侧电路一样极化二极管，它不会发光，因为没有电流流过它。因此，电压表上的读数约为零。您可以使用普通万用​​表测量它，或者在下面的示例中使用Arduino UNO R4 Minima进行测量：

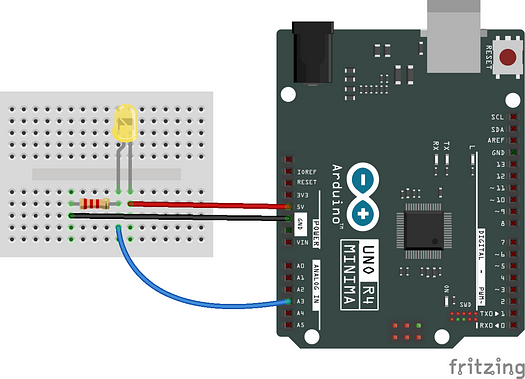
使用 Arduino 而不是普通万用表的原因是它允许我介绍这个平台。Arduino UNO R4 Minima有六个模拟输入，每个输入都可以通过集成的模数转换器( ADC ) 进行数字化，分辨率高达 14 位。

以下是一个简单的草图，将其用作 14 位万用表，对电压进行 1000 次连续测量的平均数：

// SPEED 是 USB 的波特率
#define SPEED (9600)
// C 是 ADC 计数值与电压之间的转换系数
#define C (5./16383)
// N 是用于平均的测量次数
#define N (1000)
/*
V0---C|---[   ]---|GND
*/

void setup() {
  Serial.begin(SPEED);
  analogReadResolution(14); // 将 ADC 分辨率设置为 14 位 (16383)
}

void loop() {
  float VPHOTO = 0.;
  for (int i = 0; i < N; i++) {
    VPHOTO += analogRead(A3)*C; // 获取光敏 LED 两端的电压
  }
  VPHOTO /= N;
  Serial.print("6 8 ");
  Serial.println(VPHOTO*1000);
}

代码说明（您可以跳过）该setup()函数包含在运行开始时要执行一次的语句。它将 ADC 分辨率设置为 14 位。在 中loop()，我们通过读取模拟引脚 A3 并将其乘以 ADC 计数和伏特之间的转换因子来对电阻两端的电压进行 N 次测量。

运行它并用串行绘图仪查看输出，保持 LED 处于阴影中，您应该看到类似下图的内容。绿线代表电压输出（在本例中略大于 6 mV）。

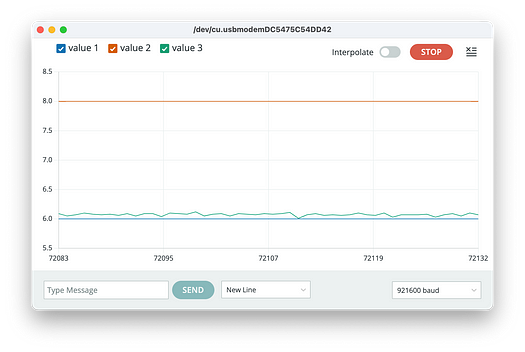
6.0 和 8.0 处的两条线是由 产生的Serial.print("6 8 ");，用于保持垂直刻度固定。

将 LED 移到阳光充足的地方，您应该会看到以下现象：

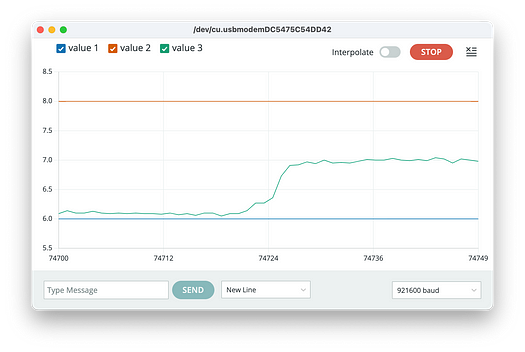
电压表读数明显增加。这意味着 LED 传导了一定的电流。这个电流从何而来？对这种现象 (光电效应) 的解释如下：当光线照射到 LED 上时，它会将能量转移到组成它的半导体的电子上，从而损失能量。电流由这些被外部电压加速的高能电子产生。它们被释放到 LED 的材料中，极化电压使它们沿着电线移动。只有当光的波长低于某个阈值 (即频率高于阈值) 时，才会发生这种现象。您可以使用带有透明盖的 LED 来测试这种行为。这种黄色 LED 在红光照射下不会发射电子，而在蓝光照射下则会发射电子。对于这种现象的唯一解释是，光是由能量为E=hf的量子（光子）组成，其中 f 是光的频率，h是称为普朗克常数的常数。

测量普朗克常数

LED 只有在被足够高的电压极化时才会发光。理想情况下，如果直接极化的二极管（上图左侧的二极管）中的极化电压低于某个阈值，则它表现为开路，电路中流动的电流I为零。当偏置电压超过阈值时，理想二极管表现为短路。实际二极管表现为非常量电阻器，电流是极化电压的函数：I = f(V)。我们可以使用 Arduino UNO R4 Minima 对 LED 进行极化，利用其 14 位DAC（数模转换器），让我们以 5/(2¹⁴-1)=5/16383≃0.3 mV 的步长产生 0 到 5 V 之间的电压。当 DAC 电压超过其阈值时，LED 会亮起，具体亮起颜色取决于其颜色。因此，我们可以构建以下设置：

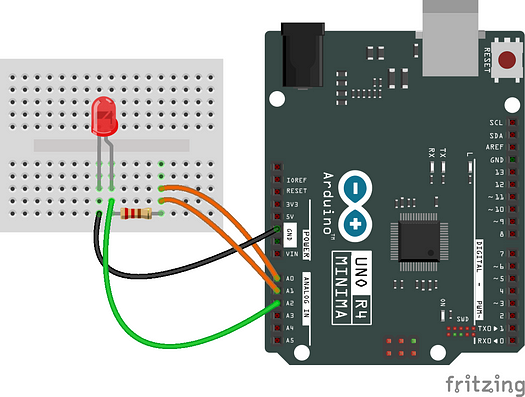
DAC 输出位于 A0 引脚。A1 引脚测量输出V ₀，而 A2 测量 LED 两端的电压 Vₗ。因此，电路中流动的电流为

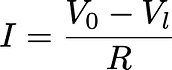
其中R =220 Ω 是与红色 LED 串联的电阻。下图逐渐增加偏置电压 ( Vi)，将其测量为V ₀ ( V0) 以及V ₗ ( )，使用欧姆定律VLED计算电流I ，并在从 0 变为 16383时输出所有这些数据：Vi

// C 是 ADC 计数值与电压之间的转换系数
#define C (5./16383)
// R 是电阻值
#define R (220.)
// SPEED 是 USB 的波特率
#define SPEED (9600)

/*
V0----[   ]---D---|GND
             |
             VLED
*/

int Vi;  // Vi 用于设置输入电压

void setup() {
  Serial.begin(SPEED);
  analogReadResolution(14); // 将 ADC 和 DAC 分辨率设置为 14 位 (16383)
  analogWriteResolution(14); 
  Vi = 0;
}

void loop() {
  analogWrite(A0, Vi);  // 设置输入电压
  float V0     = analogRead(A1)*C; // 获取实际输入电压
  float VLED   = analogRead(A2)*C; // 获取 LED 两端的电压
  Serial.print(Vi);
  Serial.print(",");
  Serial.print(V0);
  Serial.print(",");
  Serial.print(VLED);
  Serial.print(",");
  float I = (V0-VLED)/R*1000; // 计算电流（单位：mA）
  Serial.println(I);
  Vi += 1;
  if (Vi > 16383) { // 如果 Vi 超过最大值，则进入死循环
    while (1) {   
    }
  }
}

该analogWrite()函数设置 A0 上的电压值：写入从 0 到最大允许值的整数对应 0 到 5 V 之间的电压。

让我们用不同颜色的 LED 进行实验：蓝色、绿色、橙色和红色。绘制I作为V的函数，结果如下：

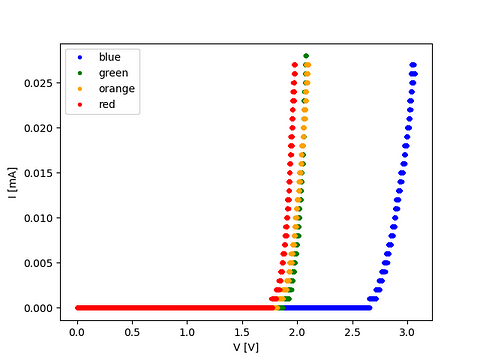
图表说明了 LED 的预期行为：电压低于 2 V 时，红色、橙色和绿色 LED 开始导通，电流随电压快速增加。当 LED 直接极化时，其电子被激发到能态E=E ₀ +qV，E ₀ 为基态，q= 1.6×10⁻¹⁹ C 为电荷，V为偏置电压。

假设一个电子处于给定的能量状态。如果其能量高于E ₀，它就会失去能量。传统上，它在导线内移动并与其组成原子碰撞，不断失去能量。电池提供将新电子提升到给定状态所需的能量，使它们在导线中流动。

实际上，电子的行为符合量子力学，电子在原子中的能态是离散的。在半导体中，能态非常密集，构成几乎连续的能带，这些能带被禁带隔开，禁带包含电子无法达到的能态。半导体导带最低能量中的电子只能以等于带隙E的离散能量单位损失能量。一旦电子损失的能量足以达到导带的下限，它只有在一次过程中损失的能量等于其当前能量与基态能量之差时，才会落入基态。能量守恒是由频率为f的电磁辐射（即能量为hf=E的光子）的发射来保证的。因此，只有当qV ₀ =hf时，才会发光，其中V ₀ 是电子获得的能量恰好等于基态能量加上带隙幅度时的电压。

当 LED 发光时，它们表现得像导体，因为电池必须提供其电子所损失的能量。只要qV ₀ =hf ，就会发生这种情况。

我们通过经验发现，描述电流作为电压函数的函数可以用抛物线来描述（实际上，几乎任何函数，如果足够平滑，都可以近似为适当次数的多项式）：

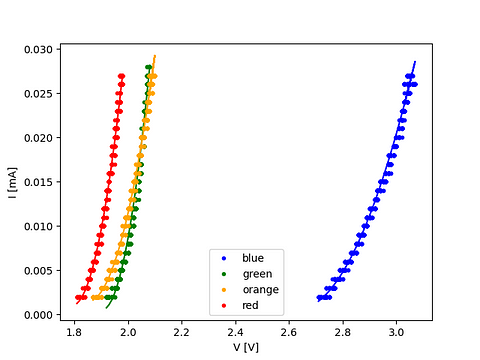
因此，我们计算了这种抛物线顶点的位置，以找到LED 开始导通时的V的准确值。通过反转上述关系，

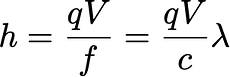
其中 c=3×10⁸ m/s 是光速，𝜆 是光波长。可以看出，蓝光需要更大的电压，因为它的波长比红光短。红色量子的能量较低。给定颜色的 LED 可以具有不同的波长，具体取决于制造商。通过对它们进行平均，我们发现

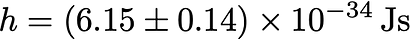
与公认值h ≃6.6×10⁻³⁴ Js 进行比较，误差小于 7%。必须注意，引用的不确定度仅指因对发射波长了解甚少而产生的不确定度。必须将测量不确定度加到其中。用于上述计算的q值的相对不确定度为 6%；3% 是c的不确定度，而 V 的不确定度可以忽略不计。最后，另外 7% 的贡献来自发射光波长的不确定性。因此，总不确定度约为 12%，所以

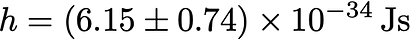
与国际单位制中定义的真实值一致

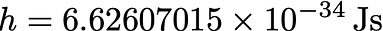
请注意，后者没有不确定性，因为普朗克常数在 SI 中被定义为定义单位。