无穷的概念一直都是自相矛盾的。如果我们滥用无穷，它仍然会带来麻烦，因此我们在数学研究中通常非常小心地对待它。罗斯-利特尔伍德悖论是最大的无穷悖论之一。它如下。

罗斯—利特尔伍德悖论

你有一个空花瓶和无限多的球。你执行无数个步骤：首先将十个球放入花瓶。接下来，从花瓶中取出一个球。你永远重复这个步骤。任务完成后，花瓶中有多少个球？

首先，如果我们必须用尽无限数量的球，任务怎么可能完成呢？我们必须在有限的时间内完成无限的步骤。假设我们需要在中午之前完成任务。

我们用数字标记这些步骤：

如果我们在中午之前2^(- n ) 分钟准确地完成步骤n，那么我们就可以完成每个步骤并在中午之前完成任务。

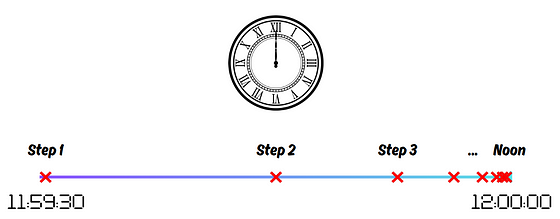
这仍然有点不舒服，但我们稍后会表达这些担忧。

罗斯-利特尔伍德悖论询问中午时花瓶里会有什么。里面会有无数个球（我们称之为满的）还是空的？也许两者都不是。这些结果怎么可能实现？我们将从满的花瓶开始，研究每种情况的论据。

花瓶已满

这是最直观的答案。每两步之后，花瓶里就会增加十个球，同时会移除一个球，所以我们净赚了九个球。无限次重复这一过程，花瓶一定会装满。

就是这样！正如我所说，这是最直观的解释——每两步额外九个球。

为了进行此论证，我们给放入的球编号。我们放入的前十个球编号为 1 到 10。接下来的十个球编号为 11 到 20。每隔一步，我们移除一个球。假设我们按升序移除它们，即我们移除第一个球，然后移除第二个球，依此类推。

到中午，花瓶就会空了。原因如下。

中午时分，选择花瓶中的任意一个球。这可以是 100 号球、1000000 号球，或者任何你喜欢的球。由于我们系统地按数字升序移除球，因此我们最终会找到你选择的球并将其移除。对于放入花瓶中的任何球，我们都会用这种方法在中午之前将其移除。

我们必须得出结论：花瓶是空的。

这种方法对“满瓶”提议提出了一个问题，但我们也可以在这里找出漏洞。假设我们按升序移除球，但从 6 号球开始。我们可以应用与上述相同的论证来得出结论，到中午时瓶中将恰好有5 个球。

尽管不可否认的是，每两步就会有九个额外的球进入花瓶，但对于中午花瓶里的东西，我们却有很多种可能的解决方案。到底发生了什么？

不出所料，问题出在问题本身！如果我们毫无疑问地接受问题设置，我们的多种解决方案都是有效的。即使在数学世界中，如果我们试图推翻这个悖论，也会发生以下两种情况之一：

为了得到相互矛盾的花瓶内容的集合，我们必须假设无限的过程终止并且我们可以在中午继续前进，但这根本不可能。

总而言之，这个问题是不恰当的，会导致多个答案，因此产生了罗斯-利特尔伍德悖论。✅

挑战 1：步骤 1：向花瓶中添加十个球并移除一个。步骤 2：向花瓶中添加十个球并移除两个。步骤n：向花瓶中添加十个球并移除n 个。在哪一步清空花瓶？

挑战 2：现在我们回到 Ross-Littlewood 悖论的设置。假设第n步需要 3^(- n ) 秒才能完成。您最多需要多长时间才能完成任意数量的步骤？