100米长的栅栏能围成的最大矩形是多少?

你手头有100米长的围栏,任务是围出一个面积尽可能大的矩形地块。围出的最大面积是多少?
在解决这个问题后,我们还会探讨如何用围栏围出最小的面积,即最大限度地降低围栏的效率。
现在,让我们解决这个问题,以下是解决方案,之后还有一些额外的挑战。

1、解决方案
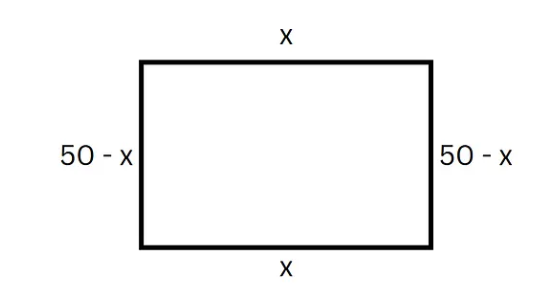
让我们用变量标记矩形的边。由于我们知道对边的长度相同,并且总周长为 100m,因此我们可以策略性地标记它们:
- 宽度为 $ x $米
- 高度为 $ 50 – x $ 米
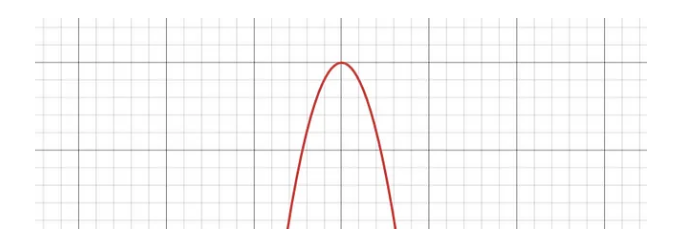
这样,矩形的周长公式为: $ 2x + 2(50 – x) = 100 \text{米} $,由于 $ x $ 的范围是 0 到 50,我们的矩形范围从铅笔到煎饼,因此我们可以确定这个标记包括周长为 100 米的所有可能的矩形。现在我们知道了宽度和高度,我们可以找到面积并最大化它。面积公式为:$ \text{面积} = x \times (50 – x) = 50x – x^2 $,由于 $ x^2 $系数为负,面积图是一条倒置的抛物线,因此在其转折点处有一个全局最大值。
2、寻找最大面积
我们将使用一个简单的技巧来找到该区域的转折点。对于二次函数 $ ax^2 + bx + c $,转折点的 $ x $ 坐标为: $ x = -\frac{b}{2a} $,在这里,$ a = -1 $,$ b = 50 $,因此:$ x = -\frac{50}{2 \times (-1)} = 25 \text{米} $,所以,矩形面积的最佳值是边长为 25 米的正方形,面积为:$ 25 \times 25 = 625 \text{平方米} $ ,我不能说我没想到它是正方形。现在来看看围栏效率最低的矩形地块。
3、最小面积
我们将使用与上面相同的公式 $ x \times (50 – x) $。当 $ x $ 接近 0 时,面积变为:$ x \times (50 – x) \approx 0 $,这将始终小于 50 $ x $ 平方米。当 $ x $ 趋向于 0 时,面积会变得任意小,因此我们可以用 100 米长的围栏有效地围住 0 平方米的面积。事实证明,你可以用无限栅栏围住仅 0 平方米的区域,但这需要深入研究分形几何,这值得写一篇文章。现在,为什么不对有限栅栏进行更多实验呢?
4、额外挑战
挑战 1:面积与周长比最大的形状是圆形。周长为 100 米的圆的面积是多少?
挑战 2: 一个圆形池塘,周长 100m,周围有一条 2m 宽的小路。小路的总面积是多少?
挑战 3: 如果将矩形缩放至周长加倍,则面积会缩小多少倍?

5、挑战的解答
挑战 1: 圆的周长公式为 $ C = 2\pi r $,面积为 $ A = \pi r^2 $。已知周长 $ C = 100 $ 米,因此半径 $ r = \frac{100}{2\pi} = \frac{50}{\pi} $ 米。面积为:
$ A = \pi \left(\frac{50}{\pi}\right)^2 = \frac{2500}{\pi} \approx 795.77 \text{平方米} $
挑战 2: 池塘的周长为 100 米,因此池塘的半径 $$ r = \frac{50}{\pi} $$ 米。加上 2 米宽的小路后,外圆的半径 $$ R = \frac{50}{\pi} + 2 $$ 米。小路的面积为外圆面积减去池塘面积:
$$ \text{小路面积} = \pi R^2 – \pi r^2 = \pi \left(\left(\frac{50}{\pi} + 2\right)^2 – \left(\frac{50}{\pi}\right)^2\right) $$
$$ = \pi \left(\frac{2500}{\pi^2} + \frac{200}{\pi} + 4 – \frac{2500}{\pi^2}\right) = \pi \left(\frac{200}{\pi} + 4\right) = 200 + 4\pi \approx 212.57 \text{平方米} $$
挑战 3: 原矩形周长为 100 米,面积最大为 625 平方米。若周长加倍至 200 米,新的最大面积对应的正方形边长为 50 米,面积为 2500 平方米。面积增加了:
$ \frac{2500}{625} = 4 \text{倍} $