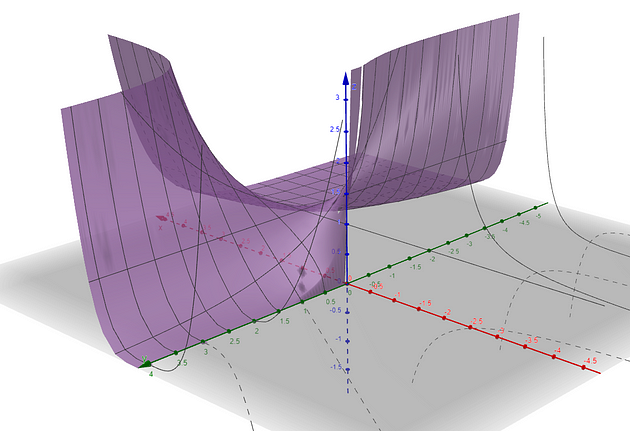
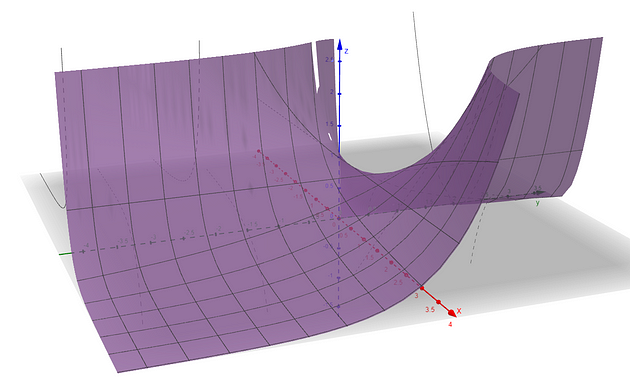
零的零次方是多少?
零的零次方不是我们所能正常计算的数。如果我们要计算一些更精确的数,比如 3⁴,我们可以取四个三的乘积:$ 3 \times 3 \times 3 \times 3 = 81 $,取零个零的乘积并不容易。我们将从两种寻找 0⁰ 的方法开始。第一种方法是固定指数。我们知道任何数的 0 次方都是 1,所以我们可以预期当x = 0 时这成立,所以 0⁰ = 1。或者,我们可以修复底座。我们知道零的任意次方都是 0,所以我们可以预期当x = 0 时这成立,所以 0⁰ = 0。
限制
要了解这里到底发生了什么,我们可以用极限来形式化这个过程。极限告诉我们当变量接近某个值时会发生什么。
- $ \lim_{x \to 0} \frac{\sin(x)}{x} $
我们不关心变量实际达到该值时会发生什么,所以我们不关心x = 0 时会发生什么。如果让x = 0,则会得到 sin(0)/0 = 0/0,这是未定义的。极限检查x接近 0 时会发生什么。
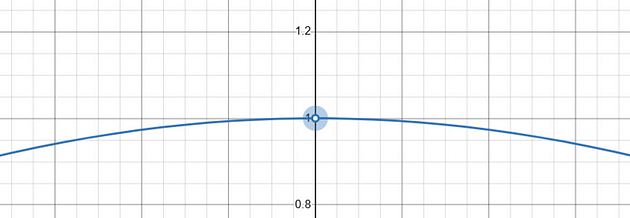
当x趋近于 0 时,我们可以看到 sin( x )/ x趋近于 1,所以这就是我们的极限,尽管 sin( x )/ x从未达到 1。它无限接近。
当x趋近于 0时,下列函数的极限是多少?
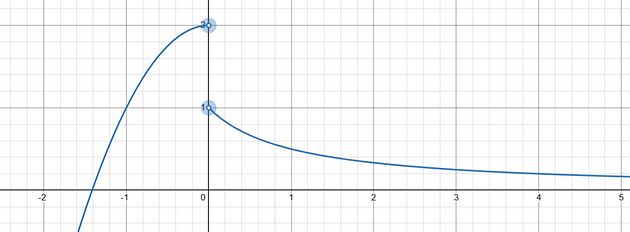
这取决于你从哪一侧取极限。x 是从左侧还是右侧趋近于 0?每种情况你都会得到不同的答案!这正是我们试图通过取极限来计算 0⁰ 时面临的问题,但它有点复杂。对于上述函数的极限,我们可以从两个方向接近x = 0:

$ \left| \lim_{(x,y)\to (0,0)} x^y \right| $
现在有了一个额外的变量,我们可以通过多种方式接近这个极限。现在我们不仅可以使用左和右,还可以使用:
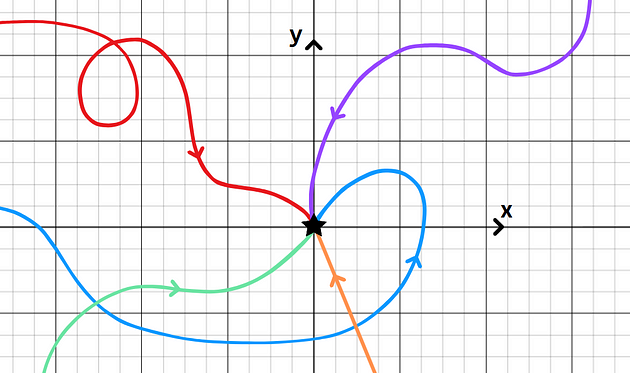
还有更多!
xʸ与我们之前看到的函数类似,根据我们采取的路径,我们会得到不同的极限。当 x 和 y 趋近于 0 时,绘制 f(x, y) = xʸ 的 3D 图形对于计算极限没有特别的帮助,但我会在文章末尾放一些图像。学习了底层数学知识后,会更好地理解它。让我们尝试沿着一些不同的路径将 ( x , y ) 发送到 (0, 0)。假设我们从顶部沿着y轴发送它。
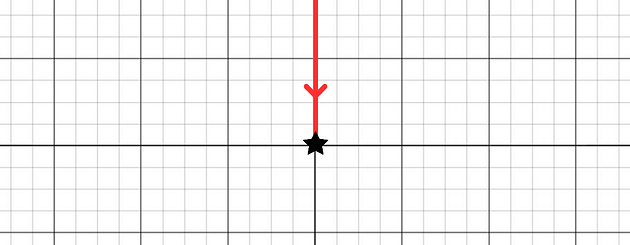
x在路径上处处为 0。我们的极限变为:$ \lim_{(x,y) \to (0,0)} 0^y = \lim_{y \to 0} 0^y $
我们不关心y = 0 时会发生什么。对于y的所有其他值,0 的y次方为 0,因此极限为 0。如果我们从底部向上接近,则此方法不起作用。您能明白为什么吗?现在我们将沿着一些不同的路径来采取限制。
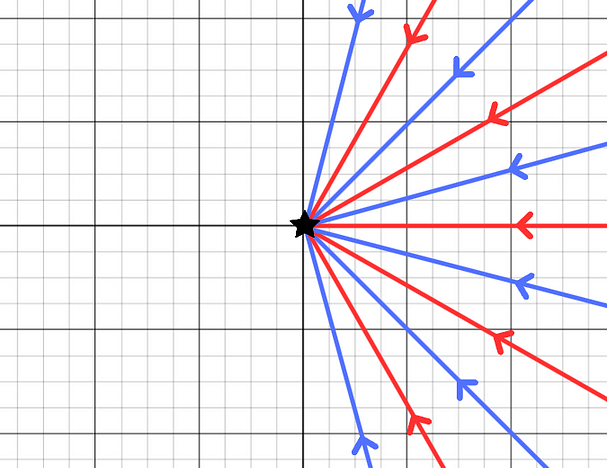
即每条非垂直线都从右侧与 (0, 0) 相交。所有这些线仅从右侧接近 (0, 0) 的原因很快就会显现出来。
每一条这样的线都可以写成y = kx ,其中k是某个数。我们可以沿着所有这些线取xʸ的极限,方法是将y替换为kx。
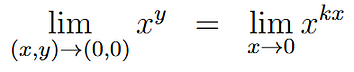
我们可以使用指数规则来处理k:
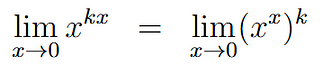
当x从上方趋近于 0 时, xˣ的极限是已知极限。
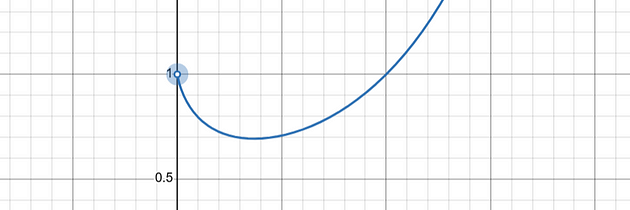
它的极限是 1,但这个极限只能从上方取,因为xˣ对于大多数负x值都是无定义的。这就是为什么我们所有的线都在 (0, 0) 的右侧 — 以确保x不会从下方接近 0。
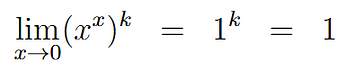
沿任意非垂直路径从右侧将 ( x , y )发送到 (0, 0) 可知当 ( x , y ) 趋近于 (0, 0) 时, xʸ的极限为 1。
另一方面,将 ( x , y ) 沿着任何垂直结束的路径发送都会告诉我们,当 ( x , y ) 趋近于 (0, 0) 时, xʸ的极限为 0。
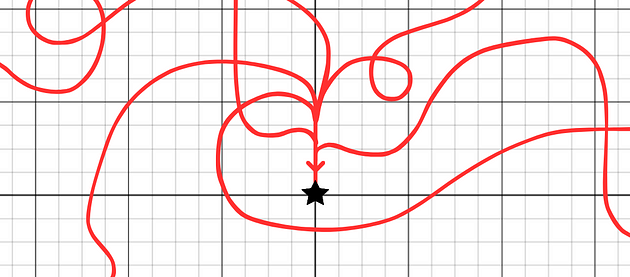
对于 0⁰,我们再次得到了两个相互矛盾的答案,但这次答案更加严格。这足以说明极限不存在。如果你从事实分析领域,你可能会说 0⁰ 是未定义的。
其他想法
0⁰ 出现在数学的其他分支中。在代数中,变量x的多项式看起来如下:
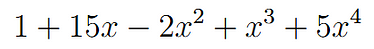
如果我们要处理任意多项式,我们不知道它有多少个项或系数是多少,因此我们用和符号来写它:

常数项是₀ x ⁰,即为了使此符号正常工作,我们需要对x的所有值都满足 x ⁰ = 1 ,因此我们假设 0⁰ = 1。
在组合学中,从大小为n的集合到大小为m的集合的函数数量由mⁿ给出。如果你有两个大小为 0 的集合(均为空),那么它们之间只有一个函数 — “空函数”。我们还在组合学中将 0⁰ 定义为 1。
人们普遍认为 0⁰ = 1,因为当我们假设这一点时,一切都会奏效。分析师对多项式使用与代数学家相同的定义,因此尽管不存在极限,他们甚至可能假设 0⁰ = 1。
您认为 0⁰ 应该是多少?我将围绕文章中讨论的主题提出一些额外的挑战。正如承诺的那样,f ( x , y ) = xʸ的图如下所示!
挑战 1:计算当x趋近于 0 时 1/ x的上下极限。一般极限存在吗?
挑战 2:证明当 ( x , y ) 趋近于 (0, 0) 时,x ² y /( x ⁴ + y ²) 的极限不存在。
提示:之前,为了求xʸ沿直线的极限,我们代入
y = kx并将x置为 0。对于这个问题,找到一些给出不同极限的代入式,并得出结论,因此极限不存在。